Las cifras significativas de una cantidad, vienen dadas por todos los dígitos medidos con certeza, más la primera cifra estimada o dígito dudoso. El número de cifras significativas de una cantidad expresa su precisión.

La medida 5,36 m tiene tres cifras significativas.
La medida 0,037 s tiene dos cifras significativas.
La medida 4,0 cm tiene dos cifras significativas.
La medida 0,4 cm tiene una cifra significativa.
La medida 4 km tiene una cifra significativa.
La medida 4,00 s tiene tres cifras significativas

En ocasiones, para conocer el número de cifras significativas de una medida, es conveniente expresar la misma en notación científica. Supongamos que obtenemos la siguiente medida con tres cifras significativas: 4,75 m. Si la expresamos en milímetros serían 4.750 mm. Podríamos pensar que su número de cifras significativas es ahora de cuatro, lo cual no tiene sentido, pero si la escribimos en notación científica 4,75 x 103 vemos, como era de esperar, que continúa teniendo tres cifras significativas.

Operaciones aritméticas con cifras significativas

Suma: La suma de dos o más medidas no debe ser más precisa que la menos precisa de las medidas.
Ejemplo: Se tienen que sumar las siguientes medidas: 2,361 m; 8,16 m 3,1 m. Matemáticamente hablando, podríamos sumarlas de la siguiente manera,

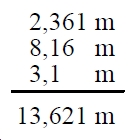
Debemos considerar que estamos sumando medidas y la operación anterior no es correcta, ya que no podemos asumir que en la medida 8,16 m la cifra de las milésimas sea un cero, pues en realidad no lo sabemos. La misma situación se presenta con la medida 3,1 m ¿que hacer entonces?, simplemente presentar todas la medidas con el mismo grado de precisión que la menos precisa de las mismas.

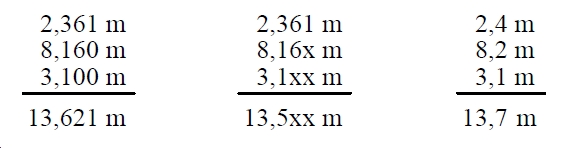
La suma de la derecha es fiable, ya que es el resultado de una suma de medidas fiables. Sin embargo, la suma de la izquierda no lo es, ya que desconocemos las cifras señaladas con x.

Resta: La diferencia de dos medidas no debe ser más precisa que la menos precisa de las mismas.
Ejemplo: Dadas las siguientes medidas 56,38 cm y 5,2 cm, encontrar su diferencia.

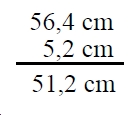
Producto: El producto de dos o más medidas no debe tener más cifras significativas que la medida que tiene el menor número de ellas.
Ejemplo: Calcular la superficie de una pieza rectangular de 4,34 m de largo por 1,2 m de ancho.

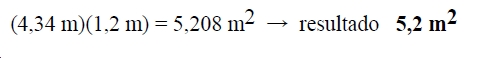
Cociente: El cociente de dos medidas no debe tener más cifras significativas que la medida que tiene el menor número de ellas.
Ejemplo: Determinar la rapidez media de un móvil que recorre 8,825 m en 2,31 s.

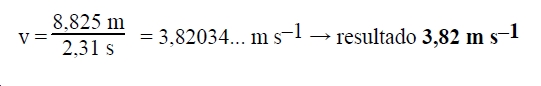
Reglas de redondeo de números

a) Si la cifra a eliminar es menor que 5, se procede a su eliminación sin más.
b) Si la cifra a eliminar es mayor que 5, se aumenta en una unidad la última cifra retenida.
c) Si la cifra a eliminar es 5, y la que le antecede es impar, se aumenta ésta en una unidad y si es par se deja como está.